Notice
Recent Posts
Recent Comments
Link
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 |
Tags
- Number()
- 소수점 올림내림
- setDate
- useState()
- sort()
- filter()
- useEffect()
- map()
- React
- 항해99솔직후기 #항해99장점 #항해99단점 #부트캠프추천
- 차집합
- Math.floor()
- getday()
- substring()
- new Date()
- indexOf()
- toUpperCase()
- 교집합
- slice()
- isNaN()
- jsx반복문
- charAt()
- repeat()
- Math.sqrt()
- 3진수
- reat if문
- includes()
- useRef()
- parseInt()
- Eventlitener
Archives
- Today
- Total
개발자로 전향중
빅오표기법의 이해 본문
👉 Big-O 표기법의 종류
- O(1)
- O(n)
- O(log n)
- O(n2)
- O(2n)

❗️O(1)

O(1)는 일정한 복잡도(constant complexity)라고 하며, 입력값이 증가하더라도 시간이 늘어나지 않는다.
- 다시 말해 입력값의 크기와 관계없이, 즉시 출력값을 얻어낼 수 있다는 의미이다.
👉 O(1)의 시간 복잡도를 가진 알고리즘
function O_1_algorithm(arr, index) {
return arr[index];
}
let arr = [1, 2, 3, 4, 5];
let index = 1;
let result = O_1_algorithm(arr, index);
console.log(result); // 2
- 이 알고리즘에선 입력값의 크기가 아무리 커져도 즉시 출력값을 얻어낼 수 있다.
- 예를 들어 arr의 길이가 100만이라도, 즉시 해당 index에 접근해 값을 반환할 수 있다.
❗️O(n)

O(n)은 선형 복잡도(linear complexity)라고 부르며, 입력값이 증가함에 따라 시간 또한 같은 비율로 증가하는 것을 의미한다.
- 예를 들어 입력값이 1일 때 1초의 시간이 걸리고, 입력값을 100배로 증가시켰을 때 1초의 100배인 100초가 걸리는 알고리즘을 구현했다면, 그 알고리즘은 O(n)의 시간 복잡도를 가진다고 할 수 있다.
👉 O(n)의 시간 복잡도를 가진 알고리즘
function O_n_algorithm(n) {
for (let i = 0; i < n; i++) {
// do something for 1 second
}
}
function another_O_n_algorithm(n) {
for (let i = 0; i < 2n; i++) {
// do something for 1 second
}
}
- O_n_algorithm 함수에선 입력값(n)이 1 증가할 때마다 코드의 실행 시간이 1초씩 증가한다.
- 즉 입력값이 증가함에 따라 같은 비율로 걸리는 시간이 늘어나고 있다. 그렇다면 함수 another_O_n_algorithm 은 어떨까?
- 입력값이 1 증가할때마다 코드의 실행 시간이 2초씩 증가한다.
- 이것을 보고, “아! 그렇다면 이 알고리즘은 O(2n) 이라고 표현하겠구나!” 라고 생각할 수 있다.
- 그러나, 사실 이 알고리즘 또한 Big-O 표기법으로는 O(n)으로 표기한다.
- 입력값이 커지면 커질수록 계수(n 앞에 있는 수)의 의미(영향력)가 점점 퇴색되기 때문에, 같은 비율로 증가하고 있다면 2배가 아닌 5배, 10배로 증가하더라도 O(n)으로 표기한다.
❗️O(log n)
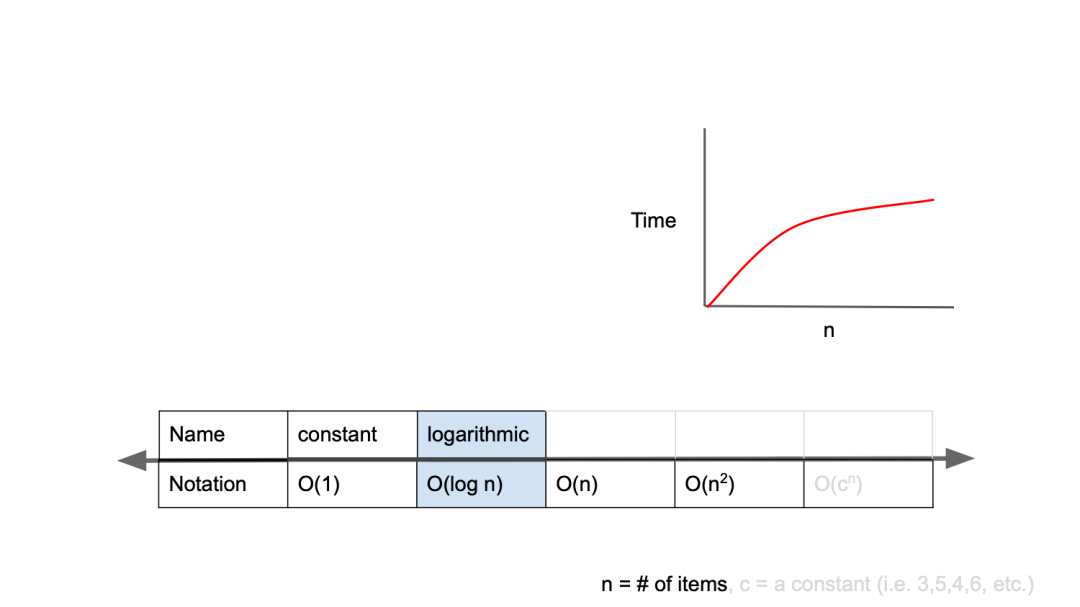
O(log n)은 로그 복잡도(logarithmic complexity)라고 부르며, Big-O표기법중 O(1) 다음으로 빠른 시간 복잡도를 가진다.
- 자료구조에서 배웠던 BST(Binary Search Tree)를 기억하는가?
- BST에선 원하는 값을 탐색할 때, 노드를 이동할 때마다 경우의 수가 절반으로 줄어든다.
- 이해하기 쉬운 게임으로 비유해 보자면 up & down을 예로 들 수 있다.
- 1~100 중 하나의 숫자를 플레이어1이 고른다. (30을 골랐다고 가정한다.)
- 50(가운데) 숫자를 제시하면 50보다 작으므로 down을 외친다.
- 1~50중의 하나의 숫자이므로 또다시 경우의 수를 절반으로 줄이기 위해 25를 제시한다.
- 25보다 크므로 up을 외친다.
- 경우의 수를 계속 절반으로 줄여나가며 정답을 찾는다.
- 매번 숫자를 제시할 때마다 경우의 수가 절반이 줄어들기 때문에 최악의 경우에도 7번이면 원하는 숫자를 찾아낼 수 있게 된다.
- BST의 값 탐색 또한 이와같은 로직으로, O(log n)의 시간 복잡도를 가진 알고리즘(탐색기법)이다.
❗️O(n2)

O(n2)은 2차 복잡도(quadratic complexity)라고 부르며, 입력값이 증가함에 따라 시간이 n의 제곱수의 비율로 증가하는 것을 의미한다.
- 예를 들어 입력값이 1일 경우 1초가 걸리던 알고리즘에 5라는 값을 주었더니 25초가 걸리게 된다면, 이 알고리즘의 시간 복잡도는 O(n2)라고 표현한다.
👉 O(n2)의 시간 복잡도를 가진 알고리즘
function O_quadratic_algorithm(n) {
for (let i = 0; i < n; i++) {
for (let j = 0; j < n; j++) {
// do something for 1 second
}
}
}
function another_O_quadratic_algorithm(n) {
for (let i = 0; i < n; i++) {
for (let j = 0; j < n; j++) {
for (let k = 0; k < n; k++) {
// do something for 1 second
}
}
}
}
- 2n, 5n 을 모두 O(n)이라고 표현하는 것처럼, n3과 n5 도 모두 O(n2)로 표기한다.
- n이 커지면 커질수록 지수가 주는 영향력이 점점 퇴색되기 때문에 이렇게 표기한다.
❗️O(2n)

O(2n)은 기하급수적 복잡도(exponential complexity)라고 부르며, Big-O 표기법 중 가장 느린 시간 복잡도를 가진다.
- 종이를 42번 접으면 그 두께가 지구에서 달까지의 거리보다 커진다는 이야기를 들어보신 적 있으신가?
- 고작 42번 만에 얇은 종이가 그만한 두께를 가질 수 있는 것은, 매번 접힐 때마다 두께가 2배 로 늘어나기 때문이다.
- 구현한 알고리즘의 시간 복잡도가 O(2n)이라면 다른 접근 방식을 고민해 보는 것이 좋다.
👉 O(2n)의 시간 복잡도를 가진 알고리즘
function fibonacci(n) {
if (n <= 1) {
return 1;
}
return fibonacci(n - 1) + fibonacci(n - 2);
}
- 재귀로 구현하는 피보나치 수열은 O(2n)의 시간 복잡도를 가진 대표적인 알고리즘이다.
- 브라우저 개발자 창에서 n을 40으로 두어도 수초가 걸리는 것을 확인할 수 있으며, n이 100 이상이면 평생 결과를 반환받지 못할 수도 있다.
[알고리즘] Time Complexity (시간 복잡도) - 하나몬
⚡️ Time Complexity (시간 복잡도) Time Complexity (시간 복잡도)를 고려한 효율적인 알고리즘 구현 방법에 대한 고민과 Big-O 표기법을 이용해 시간 복잡도를 나타내는 방법에 대해 알아봅시다. ❗️효
hanamon.kr
'자료구조&알고리즘' 카테고리의 다른 글
| [알고리즘] 브루트 포스 (0) | 2022.08.31 |
|---|---|
| [알고리즘] 탐욕 알고리즘(Greedy Algorithm) (0) | 2022.08.31 |
| 시간 복잡도(Time Complexity) 및 공간 복잡도(Space Complexity) (0) | 2022.08.29 |
| [백준] 통계 (0) | 2022.04.02 |
| [백준] 1149 RGB거리 (0) | 2022.03.25 |


